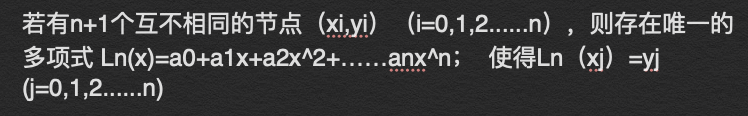目前，由武汉新型冠状病毒引起的全国肺炎疫情依旧处于肆虐爆发的时期，截止2月4日，全国累计确诊新型肺炎24324例，累计死亡490例，目前防治形势依旧严峻。自疫情爆发以来，除却一线医生以及生物医学专家在前线的战斗，后方不少专家大神也利用专业的数学模型进行疫情的建模仿真预测。作为刚入坑不久的小白，本人使用一些较为简单的数学模型，结合自己的一些思考，尝试解决提出的问题。
1 使用SIR模型进行疫情的仿真
自疫情爆发以来，多地政府迅速响应，采取封城、隔离措施，那么这些政策的有效性究竟有多大呢？本节中我主要来用相应的模型来进行论证。
1.1 SIR模型的介绍
首先来介绍一下SIR模型，SIR模型是是一种传播模型，是信息传播过程的抽象描述，广泛地应用于传染病传播模型之中。要理解SIR模型，关键点如下：
首先，模型中把传染病流行范围内的人群分成三类：S类，易感者（Susceptible），指未得病者，但缺乏免疫能力，与感病者接触后容易受到感染；I类，感病者（Infective），指染上传染病的人，它可以传播给S类成员；R类，移出者（Removal），指被隔离，或因病愈而具有免疫力的人。
理解了这个基本分类，就可以进入了模型的模拟运作环节。它的原理基于动力学提出，简单来说，它将前面总人群分的三大类别分别关于时间t建立函数，例如易感者(susceptibles)，其数量记为s(t)，表示t 时刻未染病但有可能被该类疾病传染的人数；染病者(infectives)，其数量记为i(t)，表示t时刻已被感染成为病人而且具有传染力的人数；恢复者(recovered)，其数量记为r(t)，表示t时刻已从染病者中移出的人数。设总人口为N(t)，则有N(t)=s(t)+i(t)+r(t)。
与此同时，该模型基于三个假设：
⑴不考虑人口的出生、死亡、流动等种群动力因素。人口始终保持一个常数，即N(t)≡K。
1.2 SIR模型的工作原理
上面那张知乎上的图片可以使我们直观理解模型，其实三类人群的总和就是总人数N。在这一趴中，进一步，我们给出SIR模型的数学微分表达式：
对这三个方程的解释如下，第一个方程是比较难以理解的，关键点在于理解传染率β，这个模型其实有一个隐含的条件，就是感染人群只会将疫病传染给易感人群，因此βI（t）代表这些传染源中有多少人往外界传播病毒，而S（t）/N就是易感人群所占的比例，因为已经得病的人是不会被传染的。
看完我的解释，大家再去看假设中的第二条应该就会恍然大悟，因为那儿的s，i其实就是对应着人群的比例（注意大小写，大写代表总人数，小写代表比例）
第一个方程理解了，第二个和第三个就很好理解啦！例如传染人数随时间的变化不就是两部分组成嘛（一个部分是易感人群中上升的感染者，另一部分是治愈者）
1.3 使用Matlab对新冠肺炎疫情进行模拟
要解上述微分方程，需要知道S0，I0（初值）,以及传染率β和恢复率γ。自从12.8日武汉汇报第一例确诊病例开始，设定感染人群初值为1，易感人群初值为N-1，恢复人群初值为0，N为武汉总人口数。由于该病潜伏期最大14天，设定γ=1/14。
因此难点主要在于传染率β的确定，截至目前官方尚未有任何有关数据。要解决参数问题我总结了两条思路：
1.假设所有人都是易感人群，即S=N，我们可以把这个条件带入前面SIR模型的第二个微分方程中，结合条件I（t=0）=1；最终把问题转化为求解以β为参数，t为自变量，I为因变量的方程求解，可以在matlab中求解β的最优值。
2.根据公式σ=β/γ，σ代表着病毒的基本传染数，它是衡量传染病传染性的重要评价标准。根据《纽约时报》的报道，新型肺炎的平均传染人数为1.5-3.5人（见下图，横轴为平均传染人数，纵轴为致死率，可以发现肺炎的传染率强于非典，但致死率小于非典，这和国内很多专家的判断一致）
在我的模型中，我采用第二种方法，取平均传染人数为2.5代入计算，得到β=0.1786。由此在matlab上进行仿真，下面是程序代码和运行结果
function [y ] = sir( t,x )
%SIR 此处显示有关此函数的摘要
% 此处显示详细说明
a=0.1786; %β值
b=1/14; %γ值
y=[-a*x(1)*x(2);a*x(1)*x(2)-b*x(2);b*x(2)]; %对应三个微分方程
end
clear,clc
[t,x]=ode45('sir',[0:2:150],[0.99,0.01,0]); %常微分方程求解，并输初值
plot(t,x(:,1),'-',t,x(:,2),'*',t,x(:,3),'+');
legend('易感人群','传播人群','恢复人群');
xlabel('天数');
ylabel('人群占比');
title('自然状态');
1.4 SIR模型的优缺点分析与总结
SIR模型的优点就是比较简单，并且很直观地展现了疾病传染的过程。
但SIR模型由于其过于理想化，例如模型对人群的分类不够细致，没有明确考虑隔离的因素。而现实中对疑似病人的隔离是控制疫情传播的有效手段。模型没有引入反馈机制，在预测过程中，单纯依据已有数据预测未来较长一段时间的数据，必然会使准确度降低。此外，微分方程组求解较为困难，且对初值比较敏感，这对模型的稳健性是一个很大的影响。
因此，直接用SIR模型做预测准确率是不够的，但是显然我们发现采取隔离措施是非常关键且必要的，同时也要向所有前线的医务科研工作者致以敬意，期待特效药的早日诞生!
2 使用插值法观察疫情初期是否有瞒报漏报现象
相信很多朋友和我一样，十分关心数据的准确性问题，即疫情爆发时期各地政府是否存在瞒报漏报的现象，我在本节中选用了武汉的从1.11开始上报国家卫健委以来至1.29号的数据，使用插值法进行观测。
2.1 插值法的概念介绍
插值法的概念如下：设函数y=f(x),在区间[a,b]上有定义，a<=x0<=x1<=x2…<=xn=b,对应值为y0,y1,…yn。若存在一简单函数P(x)，使p(xi)=yi (i=0,1,2,3…n),则称p(x)为f(x)的插值函数，求p（x）的方法称为插值法。因此插值法常用来解决离散数据的估计问题。
简单理解就是，已知了有限个点，我们可以求出完全经过这些点的对应函数。（注意：一定是完全经过的！）
2.2 插值法的方法简介
插值法有很多种，首先比较经典的方法就是用
多项式进行插值
。我总结的多项式定理如下，：（可以通过构造系数矩阵，利用范德蒙德行列式不等于0,矩阵方程有唯一解证明）
具体实现可以通过拉格朗日插值法来实现，方法如下：
最后再介绍一种埃尔米特插值，不少实际的插值问题不但要求在节点上的函数值相等，而且还要求对应的导数值也相等,甚至要求高阶导数也相等，满足这种要求的插值多项式就是埃尔米特插值多项式。
2.3 使用分段三次埃尔米特插值观察疫情数据
综上，我主要使用分段三次埃尔米特插值的方法去观察疫情的数据。具体的方法如下：
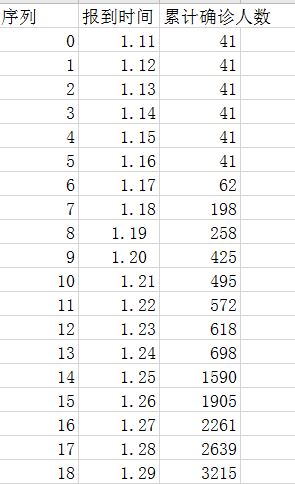
首先构建数据集，我选用自1.11号到1.29号的武汉市疫情统计数据（来源于国家卫健委官网，github上也有类似的清洗好的数据），数据如下：
具体观察的方法如下，取序号为0，2，4…18（即1.11，1.13…）的数据为原始真实数据，使用插值法，预测序号为1,3,5,6,9…17(即1.12，1.14…)的数据，比较预测值和真实值得误差，从而判断是否存在大范围的瞒报误报情况，matlab代码如下：（首先要在工作区新建矩阵x，导入上述表格中的数据）
a=[1:2:19]'; %真实值序号，等差值为2，并转为列向量
y=x(1:2:19,:); %真实值
new_x=[2:2:20]'; %待预测值的序号
p=pchip(a,y,new_x); %分段埃尔米特函数
plot(a,y,'ob',new_x,p,'or'); %画图函数
[p]
hold on
grid on
legend('真实人数','插值法预测的值')
xlabel('天数序列')
ylabel('人数')
title('分段三次埃尔米特插值')
结果如下：
通过结果和原数据的比较，发现大部分的数据吻合度较高，官方上报的数据基本可靠。但在个别数据上有较大误差（例如1.16号我们预测出的数据应该是46人，但上报的数据是41人）（刚开始连续6天零增长的数据真实性存疑），（1.24号我们预测出的数据应该是1032人左右，但上报的数据是698人）。
2.4 总结
已知一些离散数据，使用插值法得到近似函数，对缺失的数据进行补全是一种行之有效又较为方便的方法。并且在数学原理上有着非常严谨的证明和苛刻的条件。
在疫情数据观测这个具体的问题上来说，它能够基本地根据已知数据进行未知数据的预测（也可以预测未来几天的数据），但是它的局限性比较明显，例如没有考虑外界动态的变化（某日疫情的突增突减具有偶然性，不像长期稳定的数据例如人口总量）。
3 展望
本章主要采用了SIR模型和插值法，对疫情爆发做了个仿真模拟以及对疫情确诊数量可靠性进行了评估，第一个模型是个经典的传染病模型，第二个是一个纯数学模型。两者的应用都有相当大的局限性，因此本文重点还是在于模型的理解和应用，至于得出结论的真实性需要时间的检验。
未来随着数据量的增大，个人的重点准备使用回归拟合等方法对确诊数据进行预测，以及利用SIRS模型对现有的SIR模型进行优化。
最后欢迎各路大神提出宝贵的意见和建议！！
我们可以发现，在自然状态下，传播人群基本呈正态分布 ，随着时间的推移，恢复的人数会高于易感人数，并且总人数之和始终不变。但是在无干预状态下，我们可以发现传播人群峰值占总人群比例非常大，达到了几乎百分之二十五的比例。
